重なり合う信号での
光通信を可能にする光直交符号

社会のさまざまな領域で
応用される組合せデザイン

「3人組で対戦するゲームを7人で遊びたい。皆が公平に対戦できる（どの人も全員と必ず1回ずつ対戦する）組合せを考えなさい」という問題が出されたとする。

これを解くには、7人から3人を選んでいくつか組を作り、各人が組に含まれる回数が一定で、かつ異なる2人が一緒の組に含まれる回数が一定である、という条件を満たさなければならない。7人に｛0,1,2,3,4,5,6｝と番号を振ると、考えられる組合せは、例えば次のようになる。

{0,1,3}, {1,2,4}, {2,3,5}, {3,4,6}, {4,5,0}, {5,6,1}, {6,0,2}

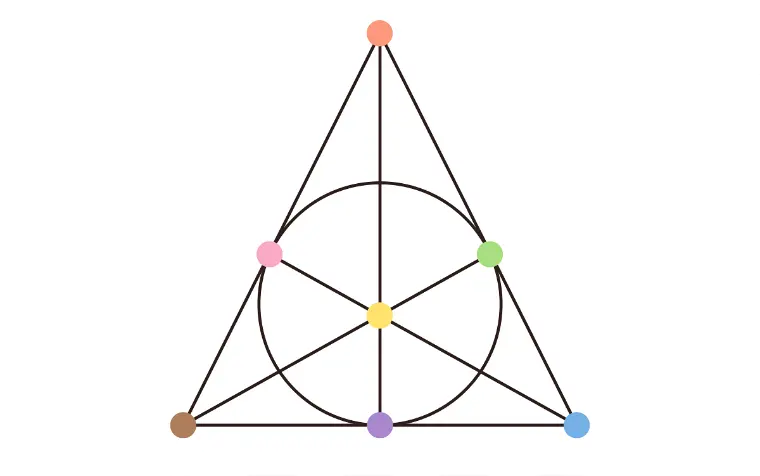
この組合せなら、0～6の全員が3回ずつゲームに参加し、かつ自分以外の6人と必ず1回対戦できる。「こうした均整の取れた組合せを見出すことを、離散数学の分野で組合せデザインと呼びます」と説明した篠原 聡教授。組合せデザインは、実社会のさまざまな領域に応用されている。伝統的な統計手法として広く活用されている実験計画法がその代表例だ。「また組合せデザインは、代数学や有限幾何といった数学分野とも密接に関わっています。先の問題の解答も、ファノ平面と呼ばれる有限射影平面に対応します」と言う［図1］。

情報通信に用いられる
光直交符号とは？

組合せデザインは、暗号技術や符号技術などの形で、情報通信にも生かされている。篠原教授は、こうした組合せデザインの情報科学への応用の一つとして、光直交符号を研究している。

「符号（コード）」とは、文章、画像、音声などの情報を数値で表したもので、情報を数値に置き換えることを「符号化」と呼ぶ。情報通信において、デジタル処理・伝送のための情報をデジタルデータに変換する際に、この符号が用いられている。「光直交符号（OOC：Optical Orthogonal Code）を用いると、光ファイバー通信で、重なり合う複数の光信号から自分宛の信号を取り出すことが可能になります」と言う。

篠原教授の解説によると、OOCは0と1の並び（符号語）の集まりであり、各符号語は自分自身との相関や、異なる符号語との相関があらかじめ設定した値以下になるという性質を持っている。つまりOOCが成立するには、次の三つの条件を満たす必要がある。

条件の一つ目は、任意の符号語において、1の数（＝重み）が一定（=w）であること、二つ目は、任意の符号語（c）に対して、cの数字を巡回的にシフト（cyclic shift）したものと、元のcを重ね合わせた時、1が重なる数（自己相関）がλa以下になること（auto-correlation property）、三つ目に、任意の符号語cと異なる符号語c’においても、それぞれ巡回シフトしたものとの1の重なり（相互相関）がλc以下となること（cross-correlation property）だ。

例えば (13,3,1)-OOC（長さ13,重み3, λa=λc=1.であるようなOOC）の符号語を考えてみる［図2］。

一つ目の符号語「1100100000000」の冒頭の1を末尾にシフトして、「1001000000001」を作る。このように一字ずつ末尾に送って巡回シフトすると、13通りの並びができる。これらの並びから二つを選び、同じ桁の位置に1が並ぶ箇所が1個以下であれば、“auto-correlation property”の条件を満たすといえる。同じように、他の符号語と比較した時、同じ桁に1が並ぶ箇所が1個以下なら、“cross-correlation property”の条件も満たすことになる。

「光通信において、多くの利用者が一つの伝送路を共有して通信すれば、混信が起きやすくなります。先の定義を満足するOOCを用いれば、複数の利用者が一つの通信路を共有しても干渉なく通信できます［図3］」

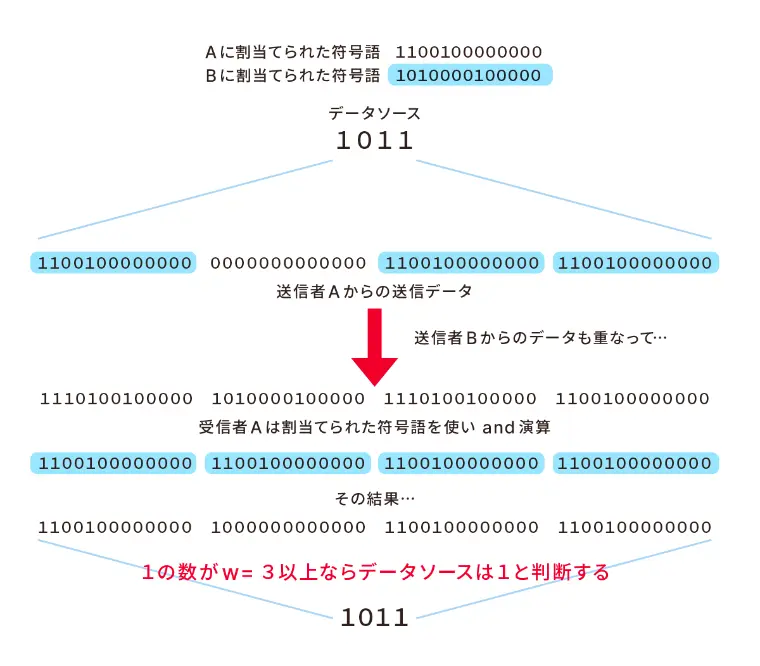
例えば通信者Aが「1011」というデータを送るとする。通信にあたって、Aのデータに符号語「1100100000000」を割り当て、「1011」を符号語で拡散して送信する。ここに符号語「101000010000」を割り当てられたBの信号が混ざったとしても、演算して1の数が3（=w）以上ならAの送信したデータソースは1だと判断できるわけだ。

射影平面上の2次曲線を
OOCの符号語に対応させる

「OOCの性能を示す指標の一つに、符号語数があります。実用性を高めるには、できるだけ多くの符号語がある方が望ましい。最大符号語数の理論上の限界が探求され続けており、この個数の符号語を持つOOCは、最適（optimal）であると呼ばれます」。篠原教授も最適なOOCを目指して多様な構成法を研究している。

中でも注力しているのが、有限幾何上の直線や曲線を符号語と対応させる方法だ。特筆すべき成果の一つが、有限幾何でいう射影平面上の2次曲線を用いて、OOCの符号語を集める方法を発見したことだ。

例えば有限幾何を使ってOOCを平面に表現すると次のようになる［図4］。

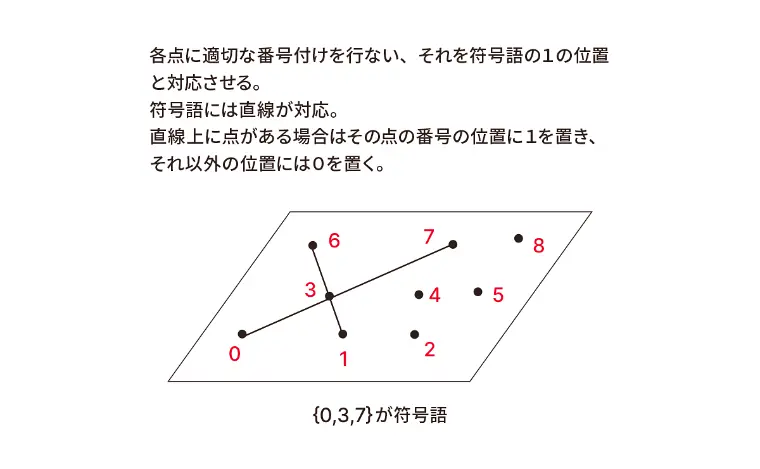
OOCにおいて同じ位置に1が現れるのは、2直線の交点で、交点が一定数以下ならOOCの条件を満たすといえる。直線同士は、必ず1点で交わるので、対応するOOCの相互相関が1になることは保証される。

「射影平面上の直線の集まりをOOCの符号語に対応させる手法は、すでに知られていました。しかし直線だけを使うと、相関を2まで許すようなOOCは構成できません。そこで、曲線を用いることを発想しました」と篠原教授。ところが射影平面上では、2次曲線同士の交点数は4以下になってしまう。これを2点以下にすることが課題だった。

篠原教授は、射影平面を拡大し、拡大体上の有限射影平面での交わり方で制限することにより、基礎体上の平面での交点数を2点以下に制御する、というアイデアで課題を解決した。「最適には至ってませんが、符号語を長くすることで、漸近的に最適に近づけることが示せました」と言う。

「実用化を念頭に置かず、数学的な興味を原動力にさらなる研究を進めたい」と篠原教授。このような基礎研究が、新たな技術革新や応用先に繋がる可能性を秘めている。情熱を持って興味・関心を追求し続けたその先にこそ、社会への応用や利活用の道も見えてくる。

2025年3月掲載

＊内容・経歴は取材もしくは執筆時のものです。