シシャモはいつ/どこに
たくさんいるのか？
限られた観測データを
解析し、推定する

中川智之

データサイエンス学環
准教授 /博士（理学）
中川研究室

中川智之准教授は、ベイズ推定を用いて空間相関のある海洋データの推定モデルを開発、シシャモの分布データからシシャモがいる時間・空間の変化を捉えることに成功。現実の複雑なデータを高速かつ効率よく解析し、現実を正確に捉えるアイデアが、データサイエンスの進展にも生かされていく。

空間相関のある海洋データの
推定モデルを開発する

数学や統計の手法を使って解析することで、単なる数字に過ぎなかったデータから、新たな知見や思いもよらない事実が見えてくる。コンピュータの発達によって、膨大なデータの計算が可能になった現代、データを集めて分析し、新しい価値を生み出すデータサイエンスの重要性はますます増している。

集めてきたデータをどのように解析すれば、求める真実を明らかにできるのか。中川智之准教授は、その手法を研究している。関心を持っているのが、「空間相関」を持つデータの解析だ。空間相関とは、例えばA市とB市の気温を見た時、両市の距離が近ければ、それだけ似たような気温になるというように、ある場所の空間的な近さが他の属性に影響を及ぼすことをいう。

最近の研究で中川准教授は、海洋データの解析手法の開発に取り組んでいる。海洋データはランダムなサンプルが少ないため、空間相関を考慮に入れて解析することが重要になるという。その一つとしてシシャモの分布データから、シシャモがいる時間・空間の変化を捉えるプロジェクトに関わった。

「2014年から2019年までの6年間、バレンツ海の約400ヵ所で観測されたシシャモのデータがあります。わかっているのは、シシャモの数と観測日、観測地点、そして観測地点の海面温度（SST）です。難点は、年によって観測日も観測地点もバラバラなことでした」。場所も時間も異なる観測データから、シシャモがいつ、どこにたくさんいるのかを推定するにはどうすればいいのか。

中川准教授らは、ベイズ推定という統計手法を使って推定モデルの構築を試みた。「ベイズ推定とは、不確実性を確率で表現し、ベイズの定理に基づき、観測したデータから推定したい事象を確率的に推論する手法です。例えば家の中でカギを探すとします。あらかじめ玄関にある確率が高そうだと予測範囲を決めてから（事前の信念：事前分布）、玄関を探します。そこで『ない』というデータを得たら、その新データをもとに新たな推論（事後の信念：事後分布）を導き出すという方法です。まず予測を立て、データを得るたびに事後分布を更新することで、現象を確率的に推論します」と説明する。従来の頻度主義的手法に対し、ベイズ推定は、サンプル数が多くなくても不確実性の評価が可能である。とりわけ空間相関や時間相関があってデータ同士が影響し合うような複雑なデータを扱う場合、非常に複雑なモデルを作る必要があるが、ベイズ推定はコンピュータを使えば解釈しやすいモデルを構築でき、スピーディーに計算できるという利点があるという。

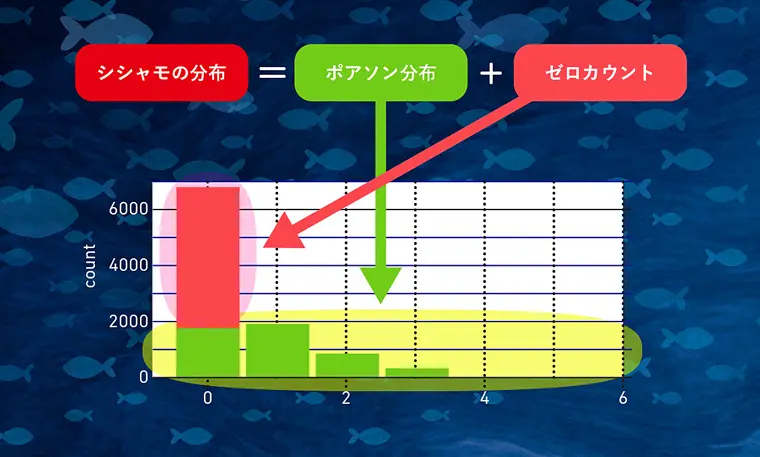
中川准教授らは、まずシシャモが全くいない（0）データが約40％もあることから、この影響を考慮に入れ、シシャモの分布を「ポアソン分布+ゼロカウント」で表すモデルに海面温度（SST）などの外生変数、空間相関と時間相関の影響を加えて、シシャモの数の平均構造を予測するモデルを考案した。これをMCMC（マルコフ連鎖モンテカルロ法）というベイズ推定の計算によく用いられる手法を使って計算し、事後分布を推定した。

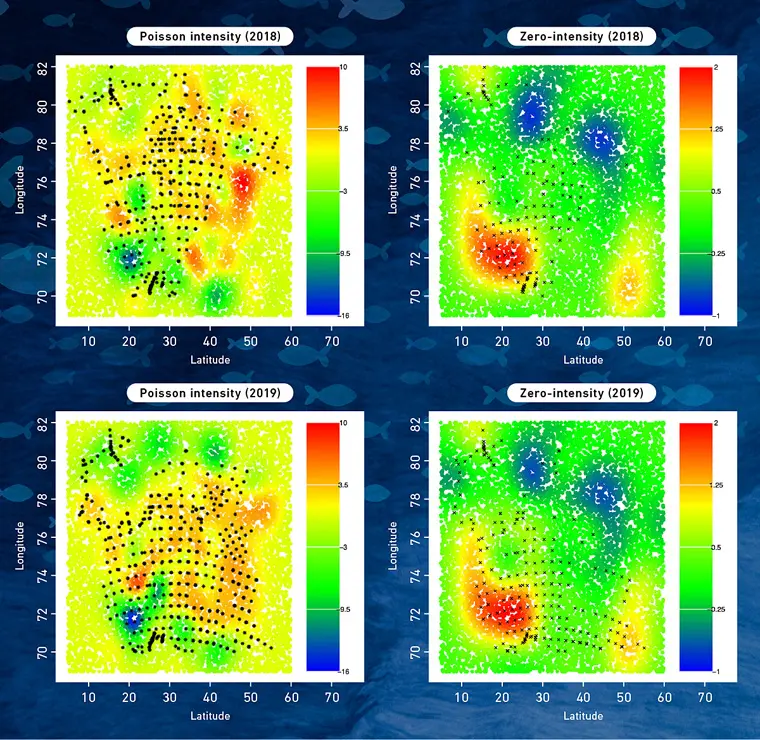
「その結果、特に目を引いたのがSSTの影響でした。水深10mの温度は、シシャモの数にほとんど影響を及ぼしませんが、水深20mの温度は、その数に影響を及ぼすことが推定できました」。こうして中川准教授らの解析結果から、シシャモの生息に関するあらたな知見を得ることができた。

図3：ポアソン分布の部分の効果（左）とゼロ過剰の部分の効果（右）（Sugasawa et al. (2022) Japanese Journal of Statistics and Data Science）

異なる変数が混在するデータから
相関構造を推定する

さらに中川准教授は、オキアミとそれを餌にするクジラの観測データから、オキアミとクジラの相関構造を捉える解析手法の開発も行っている。「このデータの特徴は、オキアミの量（連続量）と、ナガスクジラの頭数（カウント）といった性質の異なる変数が混在していることです」。中川准教授によると、多様な変数が混在しているデータから相関構造を推定するモデルは、過去の研究で構築されている。「ただし既存のモデルは、空間相関がない場合にしか適用できないため、今回のように空間相関があるデータにそのまま適用することはできません」と言う。中川准教授らは、このモデルに空間相関を考慮し、計算のアルゴリズムを工夫することで、この課題を解決することに成功した。

構築した解析手法の精度の高さが顕著に表れたのが、クジラの頭数と水深との相関関係を推定した結果である。「既存手法を用いて算出すると、クジラの頭数と水深には負の相関があるという結果が出ます。しかし自然界でこうした現象は見られないことが分かっています。一方今回考案した解析手法で推定すると、両者に相関関係は見られないと、現実を裏付ける結果になりました」